미분은 한순간의 변화량을 표시한 것이다. 표기법은 다음과 같다.
$$\frac{df(x)}{dx}=\lim_{h→0}\frac{f(x+h)-f(x)}{h}$$
함수를 미분하는 계산을 파이썬으로 구현해보자.
def numerical_diff(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)만든 미분식을 이용해 실제로 함수를 미분한 뒤 그래프로 그려본다.
import numpy as np
import matplotlib.pylab as plt
def numerical_diff(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)
def function_1(x):
return 0.01*x**2 + 0.1*x
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x,y)
plt.show()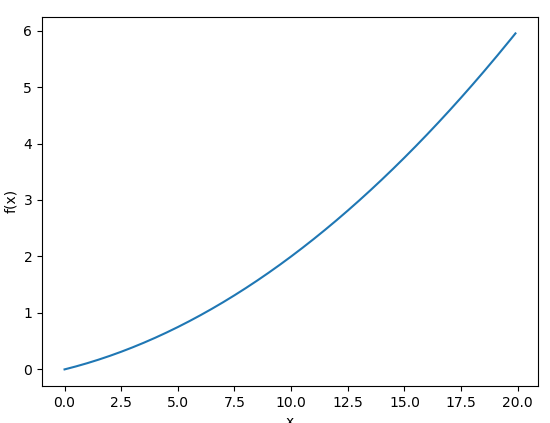
$$f(x)=0.01x^2+0.1x$$ 먼저 함수 그래프를 그려본다.
이후 미분하여 미분의 그래프를 그려본다. 머리 너무 안돌아가서 못하겠다... 난 이 길이 아닌가봄ㅎㅎㅎ~
import numpy as np
import matplotlib.pylab as plt
def numerical_diff(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)
def function_1(x):
return 0.01*x**2 + 0.1*x
def temp_inclination(f,x):
d = numerical_diff(f,x)
y = f(x) - d*x
return lambda t: d*t+y
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
tf = temp_inclination(function_1, 5)
y2 = tf(x)
plt.plot(x,y)
plt.plot(x,y2)
plt.show()
수치 미분 -> 정말 작은 값으로 미분하는 것
해석적 미분 -> 진짜 레알 수학에서 배운 미분
아무래도 0으로 향해 간다는 것을 컴퓨터는 받아들일 수 없기 때문에 이런식으로 사용하나보다. 이제 편미분을 해보자
$$ f(x_0,x_1) = x^2_0 + x^2_1 $$
def function_2(x):
return np.sum(x**2)
#retrun x[0]**2+x[1]**2그려보면 어케 생겼을까
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
def numerical_diff(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)
def function_1(x):
return 0.01*x**2 + 0.1*x
def function_2(x, y):
return x**2+y**2
def temp_inclination(f,x):
d = numerical_diff(f,x)
y = f(x) - d*x
return lambda t: d*t+y
x = np.arange(0.0, 3.0, 0.01)
y = np.arange(0.0, 3.0, 0.01)
X, Y = np.meshgrid(x,y)
# print(x[0], X[0])
Z = function_2(X,Y)
fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(X,Y,Z)
ax.view_init(elev=30,azim=50)
plt.show()그리느라 개고생했다. 3차원은 다른식으로 그려야 하는거였어...
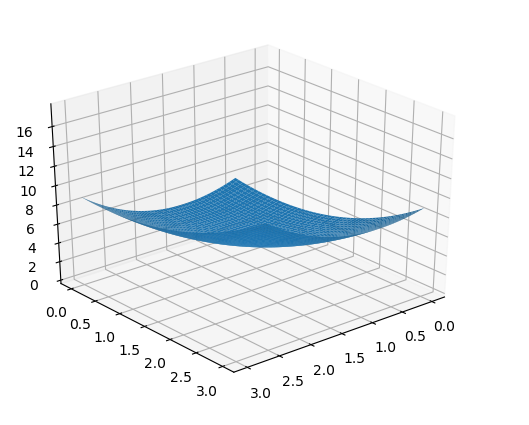
색종이같은 친구가 그려진다. 편미분은 변수가 하나인 미분과 마찬가지로 특정 장소의 기울기를 구한다. 대신 여러 변수 중 목표 변수 하나에 초점을 맞추고 구한다.
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val
return grad
def numerical_diff(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)x가 서로 다른 값일 때 편미분을 동시에 계산하기 위해서는 위 함수를 사용할 수 있다. 모든 변수의 편미분을 벡터로 정리한 것이다. 그냥 numerical이랑 비교해보면 배열 하나가 더 늘어난 것과 비슷하다. np.zeros_like(x)의 뜻은 x와 형상이 같고(길이나 타입) 원소가 0인 배열을 만드는 것이다.
x [3.0, 4.0] 이라면 tmp_val = x[0] = 3.0 을 담고 x[0] = 3 + h가 된다. f(3+h) - f(3-h) / (2*h) 를 통해 3.0의 미분을 해주고 grad에 집어 넣는다. 이 과정은 x의 길이만큼 진행해주고 미분한 만큼을 돌려주는 것이다.
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
def numerical_diff(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)
def function_2(x):
return x[0]**2+x[1]**2
def function_2_1(x):
return x**2+4.0**2
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val
return grad
print(numerical_gradient(function_2, np.array([3.0,4.0]))[0])
print(numerical_diff(function_2_1,3.0))이 둘의 값을 비교해보면 어떤 식으로 진행되는지 알 수 있다. 이 벡터들을 그래프로 그려본다.
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D
def function_2(x):
if x.ndim == 1:
return np.sum(x**2)
else:
return np.sum(x**2, axis=1)
def _numerical_gradient_no_batch(f, x):
h = 1e-4
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val
return grad
def numerical_gradient(f, x):
if x.ndim == 1:
return _numerical_gradient_no_batch(f, x)
#받은 배열이 1차원이라면 그냥 진행한다.
else:
#2차원이 넘어간다면! 차원별로 나눠주어서 진행한다.
grad = np.zeros_like(x)
for idx, x in enumerate(x):
grad[idx] = _numerical_gradient_no_batch(f, x)
return grad
if __name__ == '__main__':
x0 = np.arange(-2, 2.5, 0.25)
x1 = np.arange(-2, 2.5, 0.25)
X, Y = np.meshgrid(x0, x1)
#각각의 값으로 메쉬화 해준다.
X = X.flatten()
Y = Y.flatten()
#여러 차원의 배열을 flat하게 만들어준다.
grad = numerical_gradient(function_2, np.array([X, Y]))
plt.figure()
plt.quiver(X, Y, -grad[0], -grad[1], angles="xy",color="#666666")#,headwidth=10,scale=40,color="#444444")
plt.xlim([-2, 2])
plt.ylim([-2, 2])
plt.xlabel('x0')
plt.ylabel('x1')
plt.grid()
plt.legend()
plt.draw()
plt.show()
위 그림은 아래 식의 기울기 그래프이다.
$$f(x_0,x_1)=x^2_0+x^2_1$$
기울기가 가리키는 쪽은 각 장소에서 함수의 출력 값을 가장 크게 줄이는 방향이다.
'Python > DeepLearning' 카테고리의 다른 글
| List에 값을 append했을 때 List 전체 값이 변하는 현상 (0) | 2019.04.23 |
|---|---|
| 퍼셉트론에서 신경망으로(7) (0) | 2019.04.23 |
| 퍼셉트론에서 신경망으로(5) (0) | 2019.04.23 |
| 퍼셉트론에서 신경망으로(4) (1) | 2019.04.22 |
| 퍼셉트론에서 신경망으로(3) (0) | 2019.04.22 |


