- Basics of Statistical Process Control
- Control Charts
- Control Charts for Attributes
- Control Charts for Variables
- Control Chart Patterns
- Process Capability
1. Bascis of Statistical Process Control

SPC란 Statistical Process Control의 약자로 Product를 모니터링하여 허용 범위 이상의 quality를 감지해내는 생산 공정 모니터링이다. 한국어로는 통계적 공정 관리로 부른다. 하지만 모든 상품을 모니터링 할 수 없기 때문에 보통 샘플링을 통해 품질을 테스트 한다. 1분에 1만개의 전구를 만드는 공장을 생각해본다면, 샘플링이 왜 중요한지 알게 된다. 이 때에 무작위로 추출해내야하며 샘플은 서로 흩어져있어야 한다. 이후 이 샘플의 값을 control chart에 플로팅하고 패턴을 확인한다. 이 때에 패턴은 어떠한 표시 없이 무작위여야(정규분포를 가지고 있어야) SPC 기술의 적용이 가능하다.
비정상적인 활동이 나타난다면 두 가지 이유(Random, Non-Random)를 추측할 수 있다. 첫번째로 무작위 샘플링때문에 발생할 수 있으며 두번째로 희귀하거나 특별한 원인을 가지고 있기 떄문이다. 첫번째 이유는 일반적인 원인이며 시스템의 운영이 시작될 때부터 나타날 수 밖에 없는 필연적인 활동이다. 시스템의 개선을 통해 제거할 수 있으며 통상적인 이유를 가지고 있다. 두번째의 경우 식별 가능한 요인을 가지고 있기 때문에 운영자가 관리작업을 통해 수정할 수 있는 원인이다. SPC는 두번째 이유를 위해 운영된다.
SPC는 Attribute, Variable 두 가지 분류를 가지고 있다. Attribute는 good-bad, yes-no, pass-fail 같은 0과 1의 값을 가지고 있다. Variable은 numeric value로 target value와 실제 값의 오차를 계산하여 보여준다. 예를 들어 한 시간 동안 생산한 모니터 100대 중 5대가 불량이라면 attribute로는 95의 yes와 5의 no가 나타난 것이다. 하지만 variable로는 불량 화소의 개수를 검사해 5대 중 4대는 1개의 불량 화소를 가지고 있고 1대는 10개의 불량 화소를 가지고 있다면 총 14개의 불량 화소를 가지고 있다고 판단한다.
서비스(일반적으로 말하는 C/S)는 일반적인 SPC와는 다르다. 시간, 고객 만족도를 모니터링하면서 고객의 요구를 충족하는지 확인해야한다. 병원 업무의 경우 어떤 점들을 모니터링 해야할까? 치료가 얼마나 신속한지, 직원들이 친절하게 반응하는지, 병을 정확하게 알아내는지, 청결한지, 서류가 잘 정리되어 있는지 등등 일반적인 공정과정과는 다른 것을 확인할 수 있다.
SPC는 주로 프로세스가 제어 불능 상태가 되면 위험하고 비용이 많이 드는 작업에 적합하다. 몇 가지 예시로 공정 초기에 불량이 생긴다면 시간과 돈의 낭비가 이어질 경우, 비싼 원가를 가지고 있어 새로운 작업을 하거나 수정하기가 어려울 경우, 결함을 덮을 수 있는 작업 전후, 출하되기 직전 최종 작업 등이 있다.
2. Control Charts
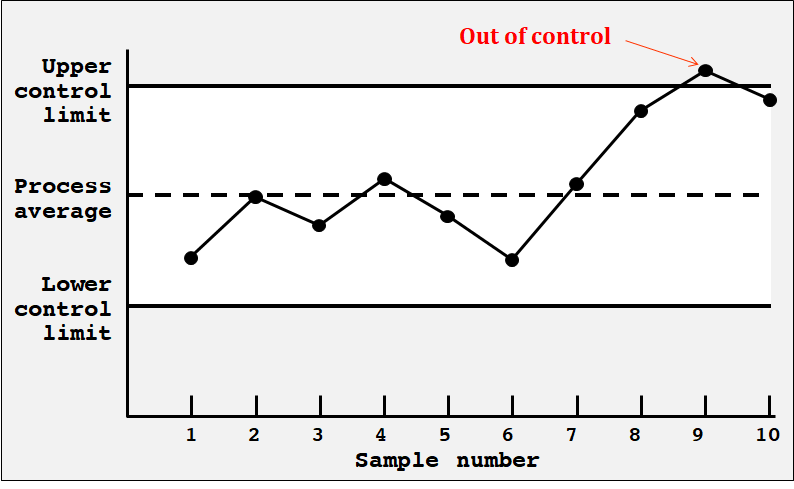
graph는 프로세스의 한계를 보여주고 이를 lower and upper로 band 형식으로 표현한다. charts는 attribute로 p-chart, c-chart가 있으며 variables로는 range(r-chart), mean(m-chart)이 있다. 이를 정규분포도로도 표현한다.
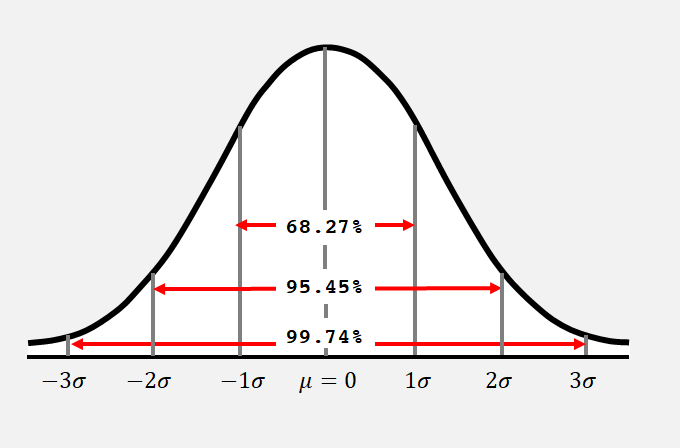
3. Control Charts for Attributes
(1) p-charts : 표본에서 결함 비율 사용

$$ z = 공정 평균으로부터의 표준 편차 $$
$$ p = 샘플 비율 $$
$$ 𝜎_𝑝 = 시료 비례 표준 편차 $$
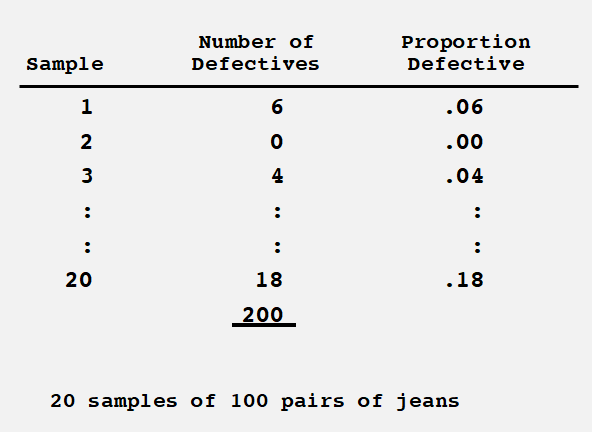
100개의 jean 중 20개의 샘플을 뽑아서 표본의 결함을 조사한다. 그리고 이 것을 적용하여본다. 계산법은 전체 결함 / sample 개수 *

이 값을 통해 lower and upper bound를 구한다.
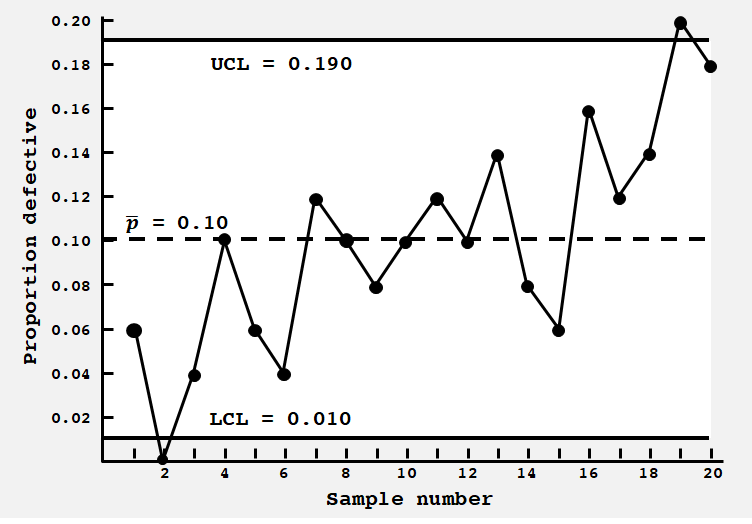
(2) c-charts : 항목의 결함 수를 사용

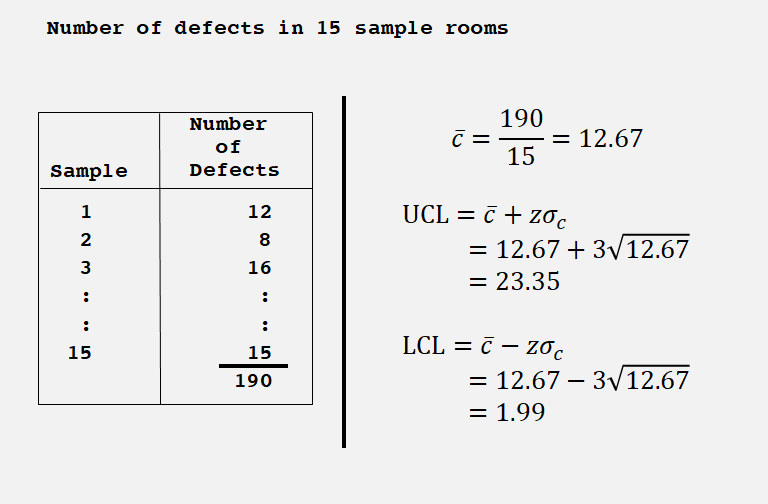
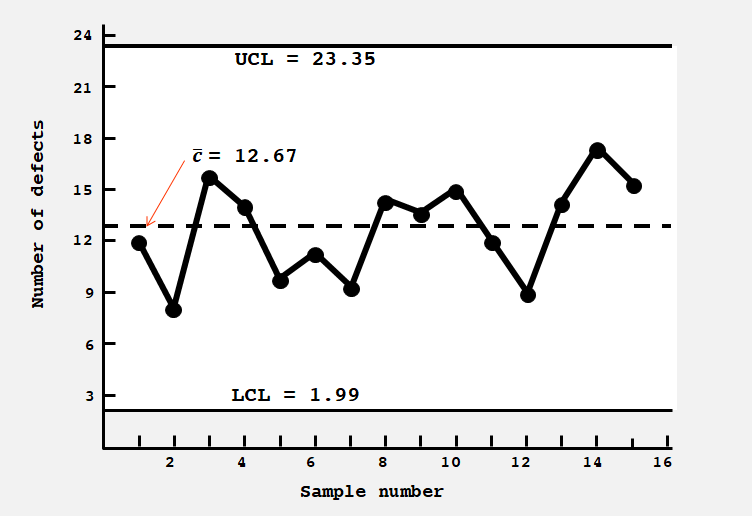
4. Control Charts for Variables
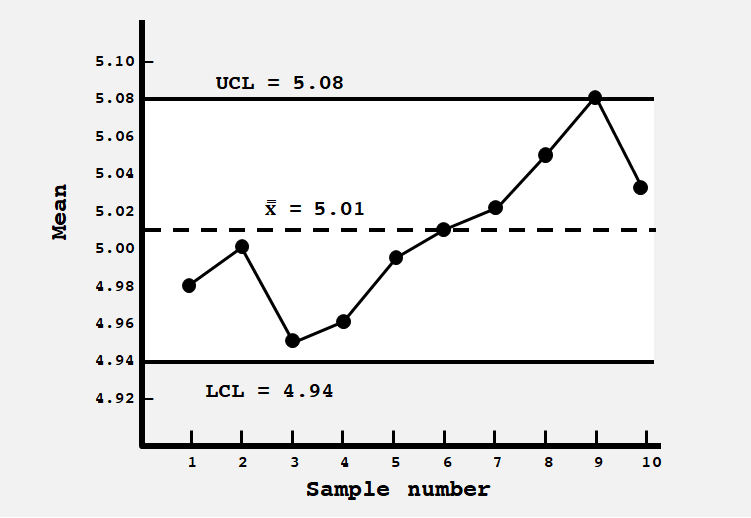
(1) Mean Chart (x ̅-Chart) : 샘플의 평균을 사용



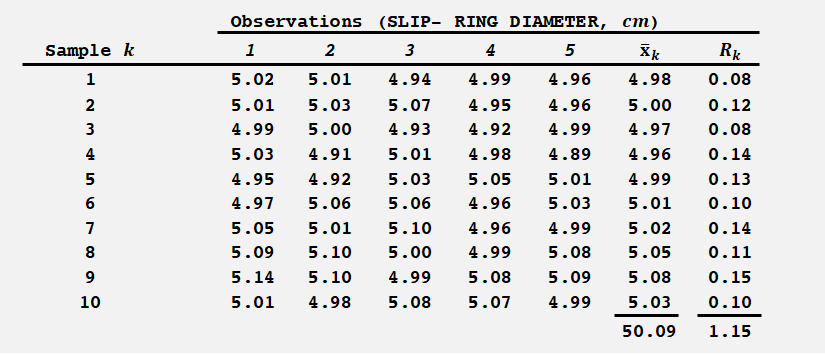
(2) Range Chart (R-Chart) : 샘플의 amount of dispersion 사용

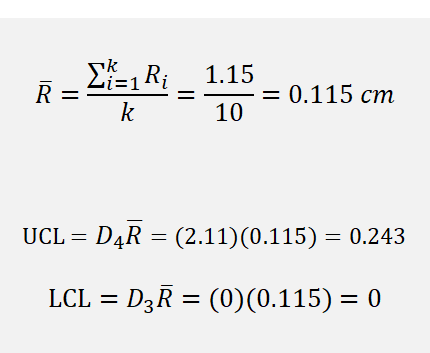
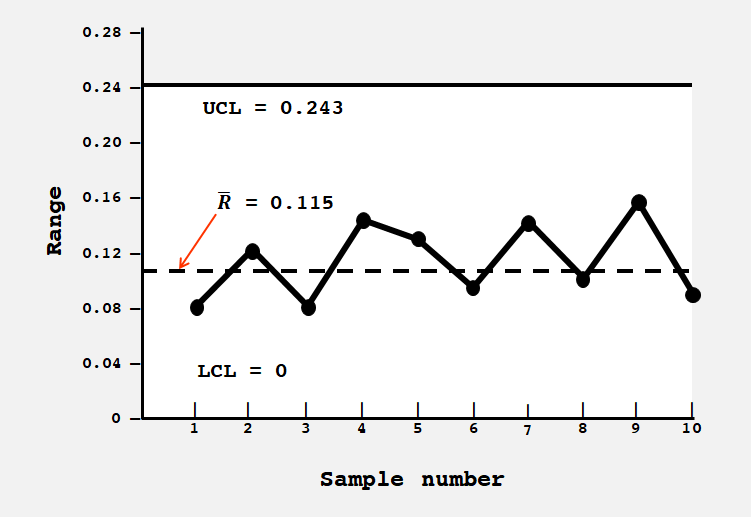
5. Control Chart Patterns
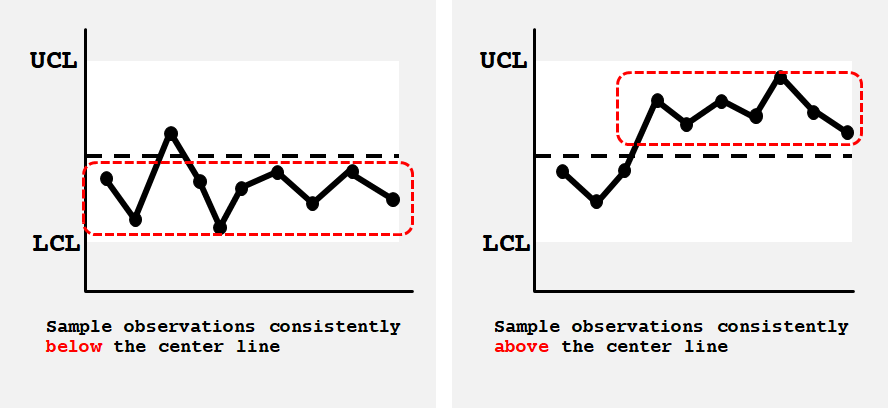
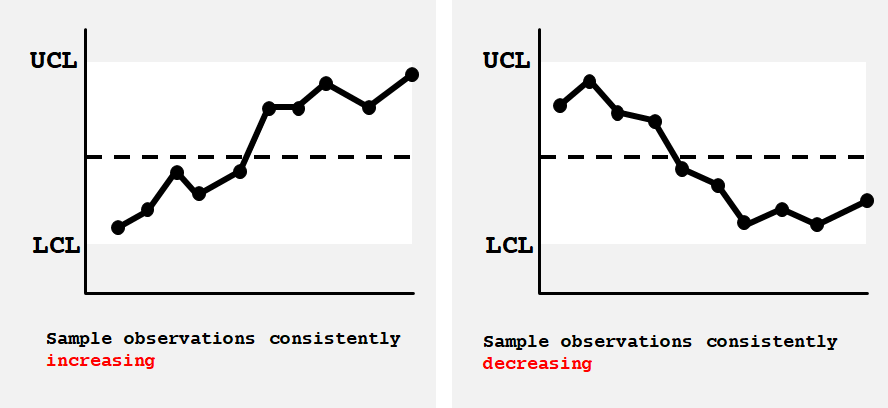
- 중심선의 한 쪽에 8개의 연속 점
- 영역을 가로지르는 8개의 연속 점
- 14개의 점이 위 아래로 번갈아가며 나타남
- 영역 A에서 3개의 연속 점 중 2개가 control limits 안쪽에 위치
- 5개의 점 중 4개가 A혹은 B에 존재
(넬슨 법칙)

- Attribute charts는 50 to 100 parts 가 샘플안에 존재해야 한다.
- Variable chart는 2 to 10 parts가 샘플안에 존재해야한다.
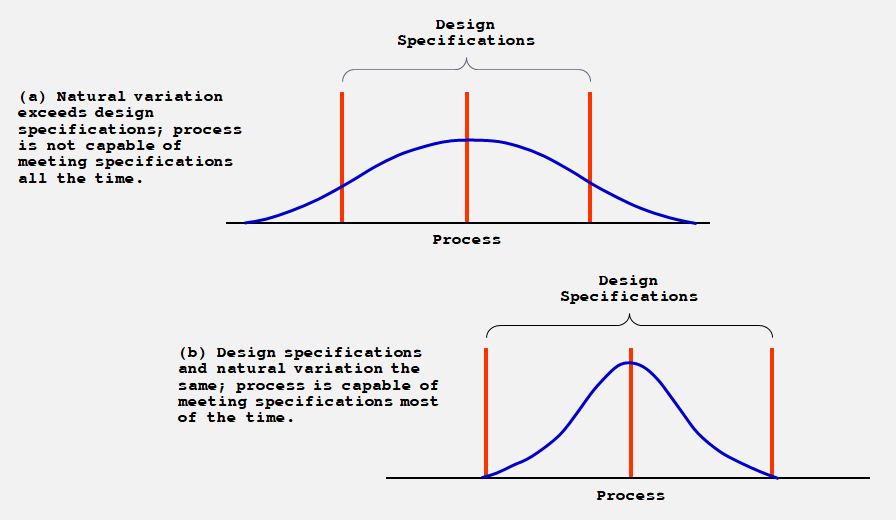
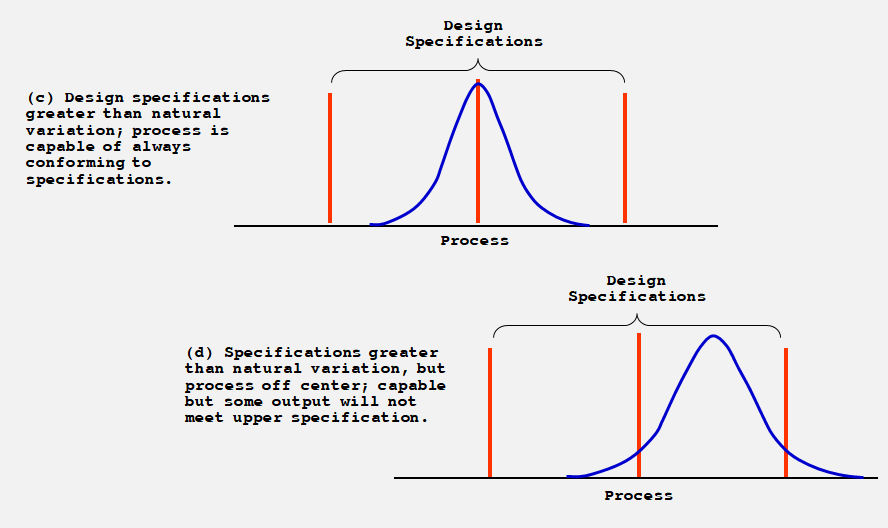
6. Process Capability (공정능력)
- Tolerances
- Process capability
'미분류 > SIDE' 카테고리의 다른 글
| INTRO TO CEPH (0) | 2020.02.11 |
|---|---|
| KendoUI를 이용하여 Range 그래프 그리기 (0) | 2019.04.03 |
| D3.js를 이용하여 하루 온/습도 그래프 그리기 (0) | 2019.03.11 |
| D3.js를 이용하여 그래프 그리기 - 선 그래프 분석 (2) | 2019.03.03 |
| D3.js 를 사용하여 그래프 그리기2 (0) | 2019.02.28 |
