특징 추출의 목적은 패턴 인식을 단순화하기 위한 정보를 추출하는 것이다. 매개 변수간의 우연한 연결로 인해 의도한 패턴이 흐트러지고 데이터가 많은수록 가짜 링크가 발생할 확률이 높아진다. Feature를 계산하면 데이터 포인트 수가 줄어들어 올바른 패턴에 집중할 수 있다. 하지만 패턴을 구분하기 위해서는 충분한 데이터가 필요하다. 체온이 높은 사람의 경우 그 사람이 운동을 하고 있는건지, 아픈건지를 판단하기는 매우 어렵다. 다른 특징을 제공하여야 상태를 구분할 수 있을 것이다. 이를 위해 많은 테스트가 필요하다.
Types of features
- Domain-specific features : 문제에 대한 지식으로 데이터를 식별
- Statistical features : 평균, 중앙값, 표준 편차와 같은 속성을 기준으로 데이터를 특성화
- Visually derived features : 시각적으로 파생된 기능으로 데이터의 패턴을 캡쳐
각 type을 알아보기위해 하나의 데이터를 불러와보자.
basedir <- "D:/Victoria/bearing_IMS/1st_test/"
data <- read.table(paste0(basedir, "2003.10.22.12.06.24"), header=FALSE, sep="\t")
colnames(data) <- c("b1.x","b1.y","b2.x","b2.y","b3.x","b3.y","b4.x","b4.y")
plot(data$b1.x, t="l")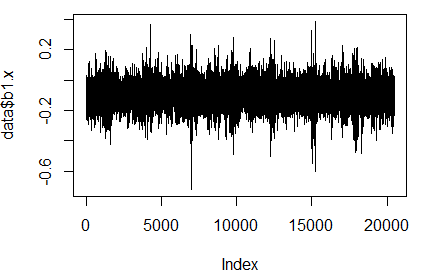
베어링 1의 x축 진동계수 그래프이다.
- Domain-specific features
베어링은 이미 많은 연구가 되어 있어 파손에 관련된 특정 유형이 분류되어 있다. ball pass outer race(BPFO), ball pass inner race(BPFI), ball spin frequency (BSF), fundamental train frequency(FTF)와 같은 네 가지 유형이 있다.
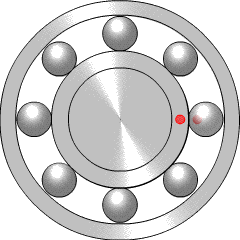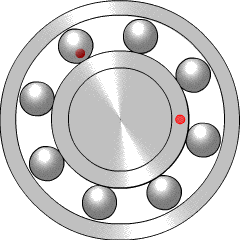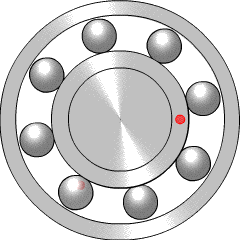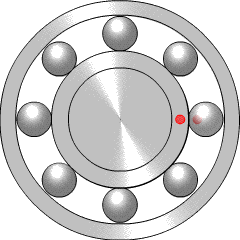
베어링은 이렇게 생겼다고 한다. 볼 중 하나에 문제가 생기면(크랙이 생기면) 접촉 시 회전의 부드러움을 감소시킨다. 크랙이 다른 볼과 접촉하게 되면 ball spin frequency가 늘어나게 된다. 만약 크랙이 내부에 생기면(붉은 점이 원주로 돌아다니는 걸 의미하는듯) BPFI가 증가한다. BPFO는 주변의 볼에 관련이 있다. 이렇게 유형에 따라 파손의 부분이 갈리게 된다.

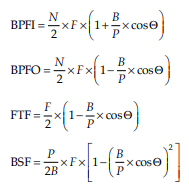

BPFO, BPFI, BSF, FTF를 계산하기 위한 방정식은 누군가 이미 실험해서 알려주었다. 그대로 가져다쓰자.
Bd <- 0.331 # ball diameter, in inches
Pd <- 2.815 # pitch diameter, in inches
Nb <- 16 # number of rolling elements
a <- 15.17*pi/180 # contact angle, in radians
s <- 2000/60 # rotational frequency, in Hz
ratio <- Bd/Pd * cos(a)
ftf <- s/2 * (1 - ratio)
bpfi <- Nb/2 * s * (1 + ratio)
bpfo <- Nb/2 * s * (1 - ratio)
bsf <- Pd/Bd * s/2 * (1 - ratio**2)확인해보자.
> data.frame(ftf,bpfi,bpfo,bsf)
ftf bpfi bpfo bsf
1 14.77522 296.9299 236.4035 139.9167fft 데이터 리턴하는 것도 저번 시간에 배웠다. 저번에는 feature로 쓰이던 top 5를 뽑아냈지만 이번에는 모든 값을 리턴하도록 한다.
fft.spectrum <- function (d)
{
fft.data <- fft(d)
# Ignore the 2nd half, which are complex conjugates of the 1st half,
# and calculate the Mod (magnitude of each complex number)
return (Mod(fft.data[1:(length(fft.data)/2)]))
}FFT의 출력은 입력의 절반을 차지하며 적용되는 주파수 범위는 0Hz에서 샘플링 주파수의 절반까지이다. 베어링 데이터의 경우 주파수 범위와 데이터가 정확히 같지 않으므로 주파수는 20,480개에서 10,240개가 되지만 샘플링 주파수는 20kHz의 절반인 10kHz이다. 실제로 frequency bin은 10,000/10,240해서 0.9766Hz라고 한다. 쉽게 만들어 보면 이렇다.
freq2index <- function(freq)
{
step <- 10000/10240 # 10kHz over 10240 bins
return (floor(freq/step))
}이후 두 개의 함수를 통해 key bearing frequencies를 계산해보자. 이것이 첫번째 4가지의 features가 된다. 첫 번째 베어링 데이터를 계산할 경우 다음과 같은 결과가 나온다.
fft.amps <- fft.spectrum(data$b1.x)
features <- c(fft.amps[freq2index(ftf)],
fft.amps[freq2index(bpfi)],
fft.amps[freq2index(bpfo)],
fft.amps[freq2index(bsf)])fft.amps에는 변환된 데이터가 들어있고 이를 다시 분할하여 features에 저장한다.
> floor(ftf/(10000/10240))
[1] 15
> fft.amps[15]
[1] 10.47455
> features[1]
[1] 10.47455이 계산은 이런 느낌이다.
> features
[1] 10.474550 6.952257 6.448870 25.312705이렇게도 계산될 수 있다. 결과적으로 변환 값 중 특정한 값을 가지고 오는 것이다.
features <- append(features, sqrt(mean(data$b1.x**2)))
> features
[1] 10.4745500 6.9522570 6.4488705 25.3127051 0.1246138Statistical features
지겹도록 나오는 정규 분포를 이용한다. 데이터의 평균 및 표준 편차를 이용하고, 평균값보다 큰지 혹은 작은지를 파악하고, 첨도(데이터의 최대치 혹은 정점 곡선)을 사용한다.
데이터를 4개로 분리하며 경계값은 5개의 피쳐를 가진다. 데이터 집합의 최소값과 최대 값은 항상 첫 번째 및 마지막 기능이며 데이터 집합의 중앙값은 세번째 기능이다. 두 번째와 네 번째는 데이터 집합의 하반 부 중앙값과 상반부로 생각할 수 있다. 무슨 소리인가 싶으니 데이터를 한 번 살펴보자.
library(e1071)
features <- append(features,
c(quantile(data$b1.x, names=FALSE),
mean(data$b1.x),
sd(data$b1.x),
skewness(data$b1.x),
kurtosis(data$b1.x)))참고로 R에서 라이브러리는 다음과 같이 다운로드 받는다.
> library(e1071)
Error in library(e1071) : ‘e1071’이라고 불리는 패키지가 없습니다
> install.packages("e1071")
> library(e1071)그렇담 지금 features에 무엇이 들어 있을까
> features
[1] 10.47455003 6.95225698 6.44887046 25.31270514 -0.72000000 -0.14600000
[7] -0.09500000 -0.04200000 0.38800000 -0.09459287 0.08112407 -0.02999057
[13] 1.06876539
> quantile(data$b1.x, names=FALSE)
[1] -0.720 -0.146 -0.095 -0.042 0.388
> mean(data$b1.x)
[1] -0.09459287
> sd(data$b1.x)
[1] 0.08112407
> skewness(data$b1.x)
[1] -0.02999057
> kurtosis(data$b1.x)
[1] 1.068765앞에서 만든 4개 + quantile, mean, sd, skewness(왜도), kurtosis(첨도) 가 들어있는 것을 확인할 수 있다.
Visually derived features
패턴을 찾기 위해서는 데이터를 시각화하는 것이다. 이전에 실험한 결과로 베어링 1과 2는 3과 4와는 조금 다른 양상을 보였다. 때문에 직감을 사용하여 이 데이터를 다시 분석해본다.
frequency <- seq(0, 10000, length.out=length(data$b1.x)/2)
plot(fft.amps[1:(length(data$b1.x)/2)] ~ frequency, t="l", ylab="Relative power")
abline(v=bsf,col="green",lty=3)
abline(v=bpfo,col="blue",lty=3)
abline(v=bpfi,col="red",lty=3)
abline(v=ftf,col="brown",lty=3)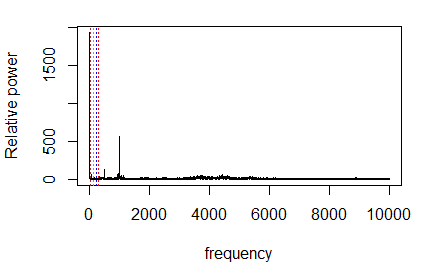
주파수를 확대하여 다시 살펴본다.
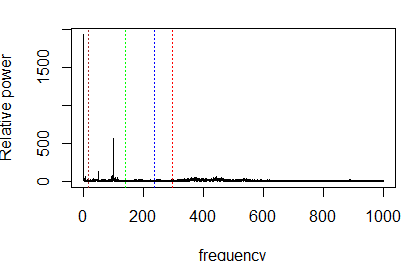
새로운 베어링은 결함과 관련된 진동 주파수를 생성해서는 안되므로 의심으로 가득차있는 3번 베어링을 살펴본다.

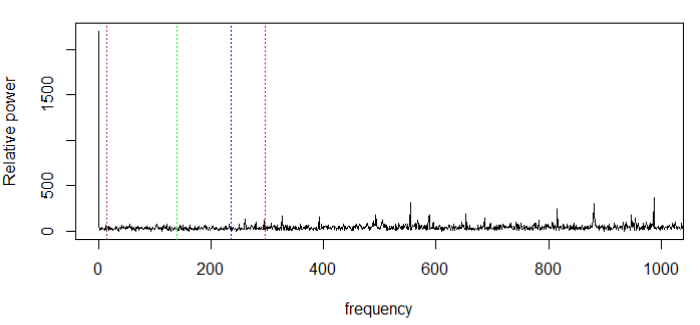
참고로 확대하려면 이렇게 작성한다.
frequency <- seq(0, 10000, length.out=length(data$b3.x)/2)
plot(fft.amps[1:(length(data$b1.x)/2)] ~ frequency, t="l", ylab="Relative power", xlim=c(0,1000))
abline(v=bsf,col="green",lty=3)
abline(v=bpfo,col="blue",lty=3)
abline(v=bpfi,col="red",lty=3)
abline(v=ftf,col="brown",lty=3)BPFI가 유의미하게 증가하고 있지만 명확하지는 않다. 주파수를 분리하기 위해 높은 주파수(VHF), 고주파(HF), 중주파(MF), 저주파(LF)로 불리는 4개의 대역으로 분리한다.
# Frequency bands
vhf <- freq2index(6000):length(fft.amps) # 6kHz plus
hf <- freq2index(2600):(freq2index(6000)-1) # 2.6kHz to 6kHz
mf <- freq2index(1250):(freq2index(2600)-1) # 1.25kHz to 2.6kHz
lf <- 0:(freq2index(1250)-1) # forcing frequency band
powers <- c(sum(fft.amps[vhf]), sum(fft.amps[hf]), sum(fft.amps[mf]), sum(fft.amps[lf]))
features <- append(features, powers)Results
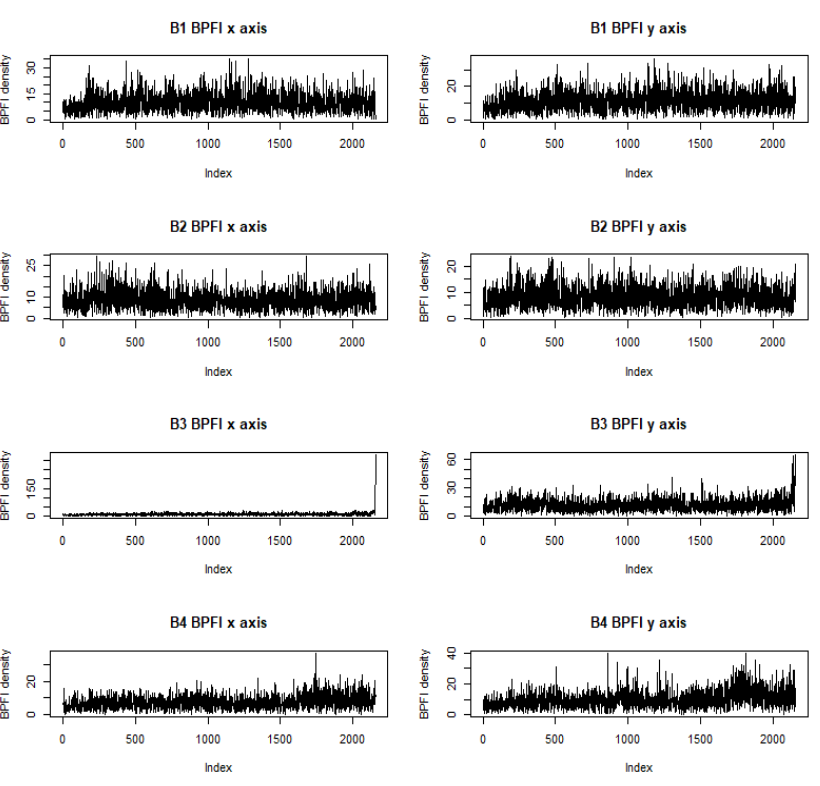
결과를 살펴보자. 먼저 BPFI를 보면 3번 베어링은 결함이 생겼기 때문에 시간이 지남에 따라 증가하는 것을 알 수 있다. 4번 베어링또한 마찬가지이다.

BPFO도 조금의 영향을 받는 것으로 보인다.
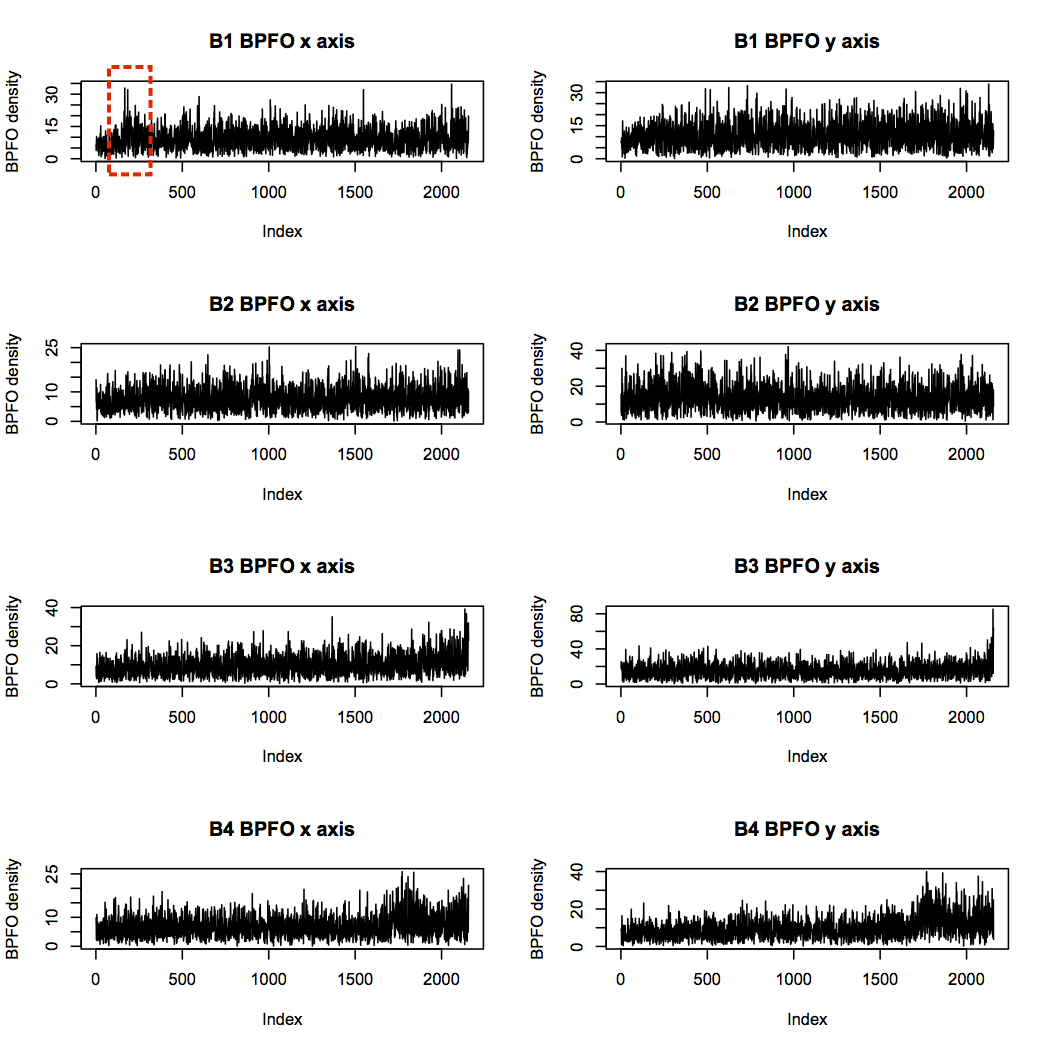
결함을 가지고 있는 B4는 높은 BSF를 가진다.
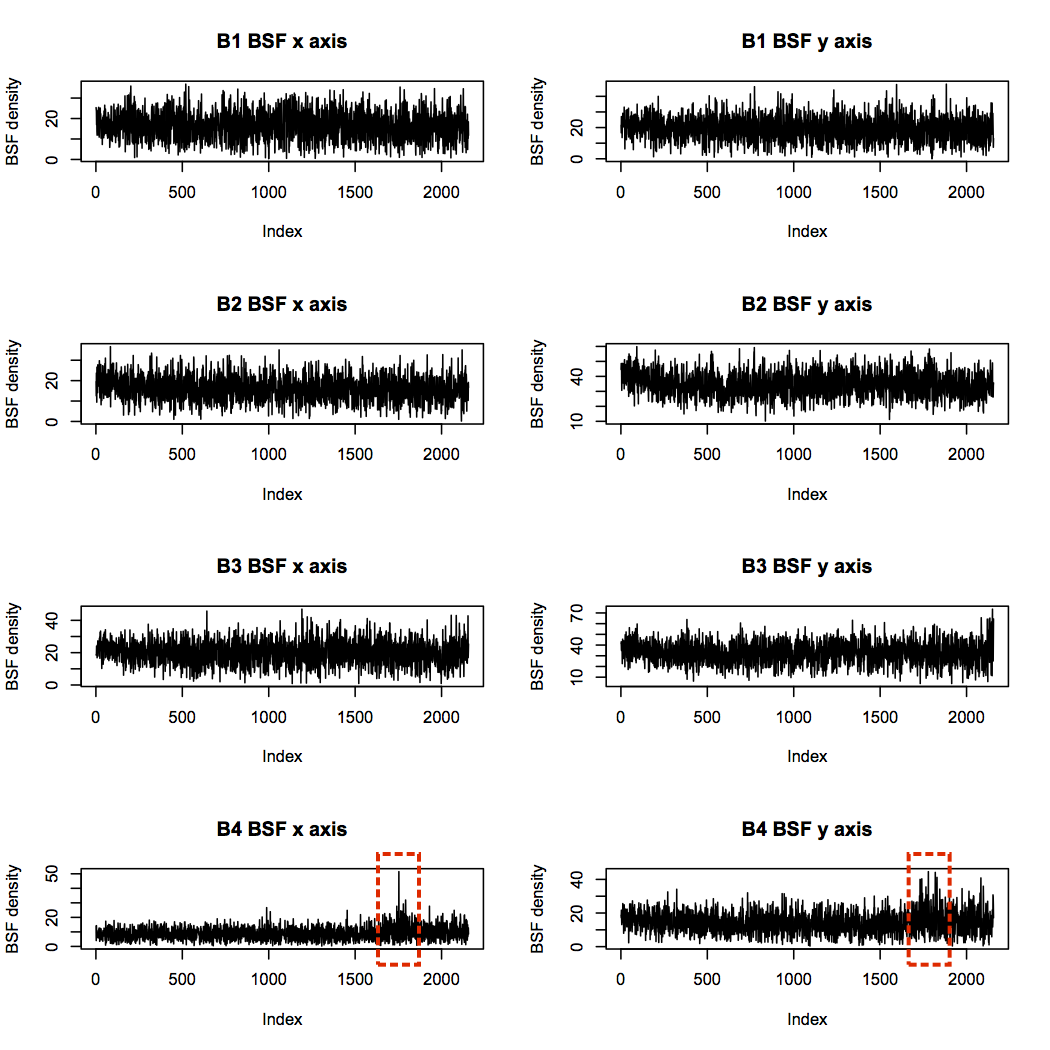
통계 기능을 살펴본다.
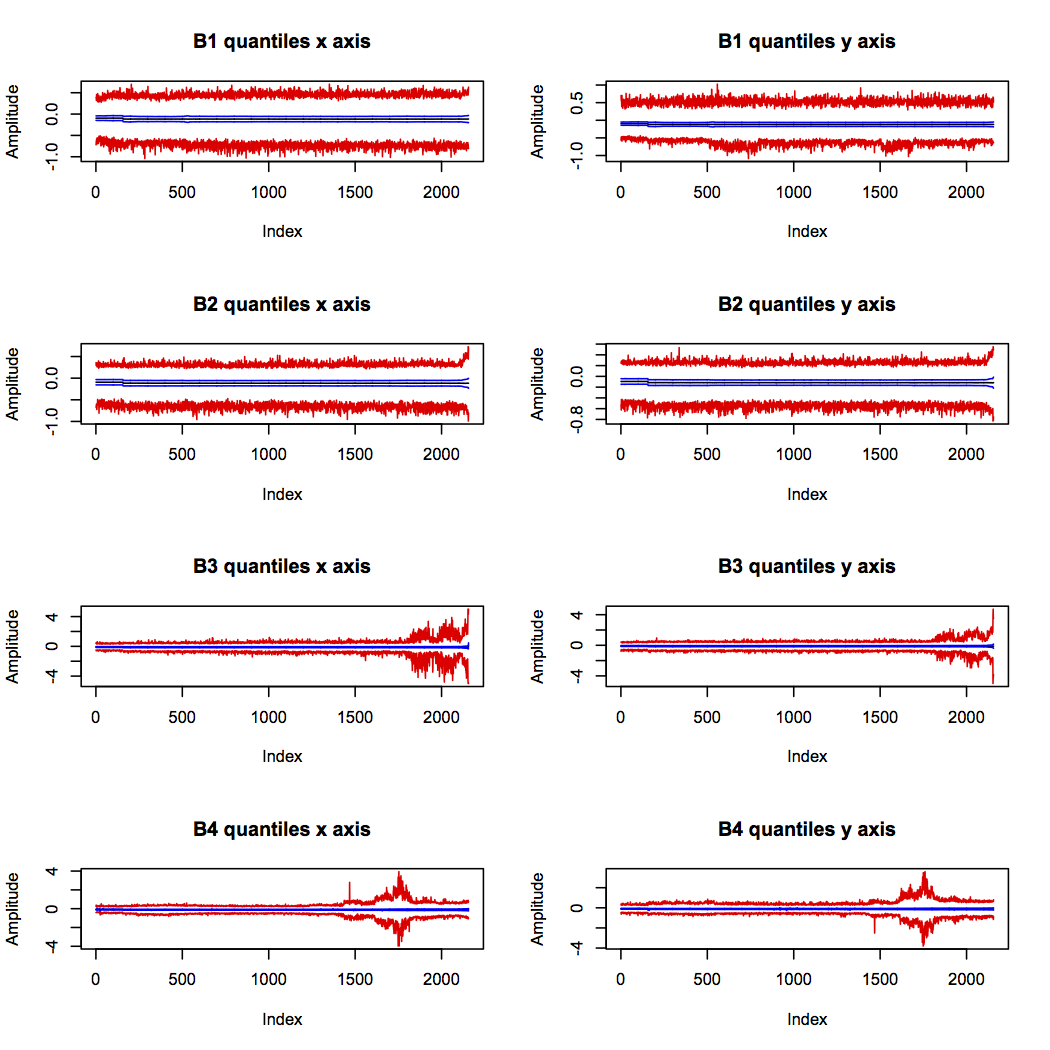
3번과 4번은 누가봐도 이상하고 2번또한 마지막 실험 단계에서 고장이 의심되는 현상을 보인다.
개인적으로 그려본 고장 이후의 그래프
알아야 하는 개념
- frequency = 주파수 = 진동수
- Nyquist frequency
수집하는 데이터는 모두 아날로그 데이터이기 때문에 컴퓨터가 처리할 수 있도록 디지털화 시켜줘야 한다. 샘플링 주파수는 입력 신호 최고 주파수의 2배 이상이 되어야 하므로 사용할 때에는 1/2배 해주는 것이다.
사용한 코드
#########################################################################
Bd <- 0.331 # ball diameter, in inches
Pd <- 2.815 # pitch diameter, in inches
Nb <- 16 # number of rolling elements
a <- 15.17*pi/180 # contact angle, in radians
s <- 2000/60 # rotational frequency, in Hz
ratio <- Bd/Pd * cos(a)
ftf <- s/2 * (1 - ratio)
bpfi <- Nb/2 * s * (1 + ratio)
bpfo <- Nb/2 * s * (1 - ratio)
bsf <- Pd/Bd * s/2 * (1 - ratio**2)
c(ftf, bpfi, bpfo, bsf)
fft.spectrum <- function (d)
{
fft.data <- fft(d)
# Ignore the 2nd half, which are complex conjugates of the 1st half,
# and calculate the Mod (magnitude of each complex number)
return (Mod(fft.data[1:(length(fft.data)/2)]))
}
freq2index <- function(freq)
{
step <- 10000/10240 # 10kHz over 10240 bins
return (floor(freq/step))
}
fft.amps <- fft.spectrum(data$b1.x)
features <- c(fft.amps[freq2index(ftf)],
fft.amps[freq2index(bpfi)],
fft.amps[freq2index(bpfo)],
fft.amps[freq2index(bsf)])
floor(ftf/(10000/10240))
fft.amps[15]
features[1]
library(e1071)
features <- append(features,
c(quantile(data$b1.x, names=FALSE),
mean(data$b1.x),
sd(data$b1.x),
skewness(data$b1.x),
kurtosis(data$b1.x)))
quantile(data$b1.x, names=FALSE)
mean(data$b1.x)
skewness(data$b1.x)
kurtosis(data$b1.x)
sd(data$b1.x)
frequency <- seq(0, 10000, length.out=length(data$b1.x)/2)
plot(fft.amps[1:(length(data$b1.x)/2)] ~ frequency, t="l", ylab="Relative power")
abline(v=bsf,col="green",lty=3)
abline(v=bpfo,col="blue",lty=3)
abline(v=bpfi,col="red",lty=3)
abline(v=ftf,col="brown",lty=3)
plot(fft.amps[1:(length(data$b1.x)/2)] ~ frequency, t="l", ylab="Relative power", xlim=c(0,1000))
abline(v=bsf,col="green",lty=3)
abline(v=bpfo,col="blue",lty=3)
abline(v=bpfi,col="red",lty=3)
abline(v=ftf,col="brown",lty=3)
fft.spectrum <- function (d)
{
fft.data <- fft(d)
# Ignore the 2nd half, which are complex conjugates of the 1st half,
# and calculate the Mod (magnitude of each complex number)
return (Mod(fft.data[1:(length(fft.data)/2)]))
}
freq2index <- function(freq)
{
step <- 10000/10240 # 10kHz over 10240 bins
return (floor(freq/step))
}
# Bearing data
Bd <- 0.331 # ball diameter, in inches
Pd <- 2.815 # pitch diameter, in inches
Nb <- 16 # number of rolling elements
a <- 15.17*pi/180 # contact angle, in radians
s <- 2000/60 # rotational frequency, in Hz
ratio <- Bd/Pd * cos(a)
ftf <- s/2 * (1 - ratio)
bpfi <- Nb/2 * s * (1 + ratio)
bpfo <- Nb/2 * s * (1 - ratio)
bsf <- Pd/Bd * s/2 * (1 - ratio**2)
fft.amps <- fft.spectrum(data$b3.x)
features <- c(fft.amps[freq2index(ftf)],
fft.amps[freq2index(bpfi)],
fft.amps[freq2index(bpfo)],
fft.amps[freq2index(bsf)])
features <- append(features,
c(quantile(data$b3.x, names=FALSE),
mean(data$b3.x),
sd(data$b3.x),
skewness(data$b3.x),
kurtosis(data$b3.x)))
frequency <- seq(0, 10000, length.out=length(data$b3.x)/2)
plot(fft.amps[1:(length(data$b3.x)/2)] ~ frequency, t="l", ylab="Relative power", xlim=c(0,1000))
abline(v=bsf,col="green",lty=3)
abline(v=bpfo,col="blue",lty=3)
abline(v=bpfi,col="red",lty=3)
abline(v=ftf,col="brown",lty=3)
# Frequency bands
vhf <- freq2index(6000):length(fft.amps) # 6kHz plus
hf <- freq2index(2600):(freq2index(6000)-1) # 2.6kHz to 6kHz
mf <- freq2index(1250):(freq2index(2600)-1) # 1.25kHz to 2.6kHz
lf <- 0:(freq2index(1250)-1) # forcing frequency band
powers <- c(sum(fft.amps[vhf]), sum(fft.amps[hf]), sum(fft.amps[mf]), sum(fft.amps[lf]))
features <- append(features, powers)
all.features <- function(d)
{
# Statistical features
features <- c(quantile(d, names=FALSE), mean(d), sd(d), skewness(d), kurtosis(d))
# RMS
features <- append(features, sqrt(mean(d**2)))
# Key frequencies
fft.amps <- fft.spectrum(d)
features <- append(features, fft.amps[freq2index(ftf)])
features <- append(features, fft.amps[freq2index(bpfi)])
features <- append(features, fft.amps[freq2index(bpfo)])
features <- append(features, fft.amps[freq2index(bsf)])
# Strongest frequencies
n <- 5
frequencies <- seq(0, 10000, length.out=length(fft.amps))
sorted <- sort.int(fft.amps, decreasing=TRUE, index.return=TRUE)
top.ind <- sorted$ix[1:n] # indexes of the largest n components
features <- append(features, frequencies[top.ind]) # convert indexes to frequencies
# Power in frequency bands
vhf <- freq2index(6000):length(fft.amps) # 6kHz plus
hf <- freq2index(2600):(freq2index(6000)-1) # 2.6kHz to 6kHz
mf <- freq2index(1250):(freq2index(2600)-1) # 1.25kHz to 2.6kHz
lf <- 0:(freq2index(1250)-1) # forcing frequency band
powers <- c(sum(fft.amps[vhf]), sum(fft.amps[hf]), sum(fft.amps[mf]), sum(fft.amps[lf]))
features <- append(features, powers)
return(features)
}
b1m <- matrix(nrow=0, ncol=(2*23))
b2m <- matrix(nrow=0, ncol=(2*23))
b3m <- matrix(nrow=0, ncol=(2*23))
b4m <- matrix(nrow=0, ncol=(2*23))
# and for timestamps
timestamp <- vector()
for (filename in list.files(basedir))
{
cat("Processing file ", filename, "\n")
ts <- as.character(strptime(filename, format="%Y.%m.%d.%H.%M.%S"))
data <- read.table(paste0(basedir, filename), header=FALSE, sep="\t")
colnames(data) <- c("b1.x", "b1.y", "b2.x", "b2.y", "b3.x", "b3.y", "b4.x", "b4.y")
# Bind the new rows to the bearing matrices
b1m <- rbind(b1m, c(all.features(data$b1.x), all.features(data$b1.y)))
b2m <- rbind(b2m, c(all.features(data$b2.x), all.features(data$b2.y)))
b3m <- rbind(b3m, c(all.features(data$b3.x), all.features(data$b3.y)))
b4m <- rbind(b4m, c(all.features(data$b4.x), all.features(data$b4.y)))
timestamp <- c(timestamp, ts)
}
cnames <- c("Min.x", "Qu.1.x", "Median.x", "Qu.3.x", "Max.x", "Mean.x", "SD.x", "Skew.x", "Kurt.x", "RMS.x", "FTF.x", "BPFI.x", "BPFO.x", "BSF.x", "F1.x", "F2.x", "F3.x", "F4.x", "F5.x", "VHF.pow.x", "HF.pow.x", "MF.pow.x", "LF.pow.x", "Min.y", "Qu.1.y", "Median.y", "Qu.3.y", "Max.y", "Mean.y", "SD.y", "Skew.y", "Kurt.y", "RMS.y", "FTF.y", "BPFI.y", "BPFO.y", "BSF.y", "F1.y", "F2.y", "F3.y", "F4.y", "F5.y", "VHF.pow.y", "HF.pow.y", "MF.pow.y", "LF.pow.y")
length(cnames)
colnames(b1m) <- cnames
colnames(b2m) <- cnames
colnames(b3m) <- cnames
colnames(b4m) <- cnames
b1 <- data.frame(timestamp, b1m)
b2 <- data.frame(timestamp, b2m)
b3 <- data.frame(timestamp, b3m)
b4 <- data.frame(timestamp, b4m)
write.table(b1, file=paste0(basedir, "../b1_all.csv"), sep=",", row.names=FALSE)
write.table(b2, file=paste0(basedir, "../b2_all.csv"), sep=",", row.names=FALSE)
write.table(b3, file=paste0(basedir, "../b3_all.csv"), sep=",", row.names=FALSE)
write.table(b4, file=paste0(basedir, "../b4_all.csv"), sep=",", row.names=FALSE)
plot(b1[, 12], ylab="BPFI density",xlab="Index", main="B1 BPFI x axis", t="l")
plot(b1[, 35], ylab="BPFI density",xlab="Index", main="B1 BPFI y axis", t="l")
plot(b2[, 12], ylab="BPFI density",xlab="Index", main="B2 BPFI x axis", t="l")
plot(b2[, 35], ylab="BPFI density",xlab="Index", main="B2 BPFI y axis", t="l")
plot(b3[, 12], ylab="BPFI density",xlab="Index", main="B3 BPFI x axis", t="l")
plot(b3[, 35], ylab="BPFI density",xlab="Index", main="B3 BPFI y axis", t="l")
plot(b4[, 12], ylab="BPFI density",xlab="Index", main="B4 BPFI x axis", t="l")
plot(b4[, 35], ylab="BPFI density",xlab="Index", main="B4 BPFI y axis", t="l")
'미분류 > R' 카테고리의 다른 글
| Understanding data science: classification with neural networks in R (0) | 2019.06.12 |
|---|---|
| Understanding data science: clustering with k-means in R (0) | 2019.06.11 |
| R 기본 (추가 중) (0) | 2019.06.05 |
| Understanding data science: dimensionality reduction with R (0) | 2019.06.04 |
| Understanding data science: feature extraction with R (0) | 2019.06.03 |



