R에서 k-means로 clustering 해보자.
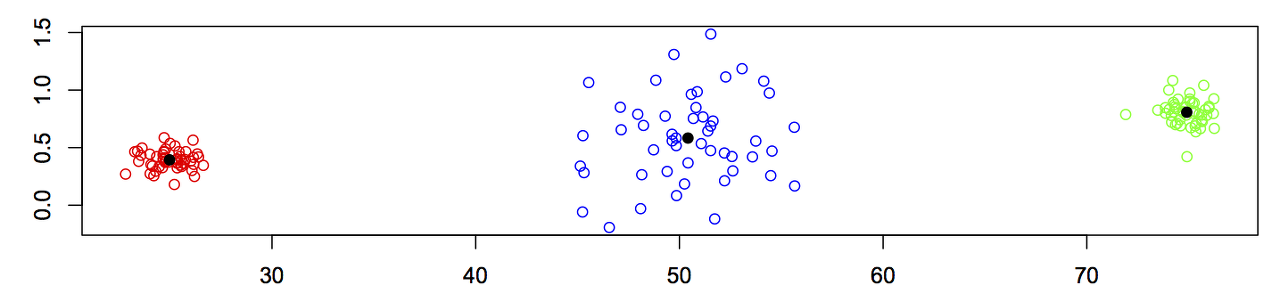
k-means clustering는 k-평균 군집화라고 불리며 군집화 알고리즘 가운데 하나이다. 군집은 하나의 중심을 가지며 개체는 가장 가까운 중심에 할당된다. k는 군집 수이다.
From features to diagnosis
분석의 목표는 4개의 베어링의 상태를 진단하는 것이다. 베어링은 수명이 다 할때까지 실행되었고 데이터는 그 기록을 가지고 있기 때문에 두 개의 베어링이 실패했다는 것을 알 수 있다. 대략적인 변화상태를 알기 위해 그래프에 라벨을 붙여 판단한다.
- green: “early” (initial run-in of the bearings)
- blue: “normal”
- yellow: “suspect” (health seems to be deteriorating)
- red: “failure.b1”, “failure.b2”, “failure.inner”, or “failure.roller”
- salmon: “stage2” (secondary failure of b4)
- black: “unknown” (unusual activity in b1)

사용할 데이터는 저번에 추출한 best 머시기이다.
# 14 features looks best. save those plus bearing and state labels
write.table(data[c("bearing", "State", sorted[1:14])], file=paste0(basedir, "../all_bearings_best_fv.csv"), sep=",", row.names=FALSE)이걸로 저장하도록 하자. 이 데이터가 담고있는 정보를 간략하게 보면 아래와 같다.

이게 어디서 나온 데이터인가 하고 생각해보면 차원 감소를 하여 나온 feature들이다. 좋은 세트인 14개의 feature vector인 것이다. 이것을 이용하여 clustring을 해본다.
K-means clustring
라벨을 알려주지 않고 데이터의 기본 구조를 나타낸다. K-means clustring은 데이터를 k개의 클러스터로 분리하여 나타낸다. 클러스터 분석은 베어링이 status1 -> status2로 넘어갈 때 데이터가 명확하게 변한다는 것을 가정하고 실험한다.
Choosing k
k-means는 unsupervised 하지만 몇 개의 클러스터로 구성되어 있는지 정도는 추리해내야 한다. 일반적으로 label 수에 가깝게 만들어지지만 여러 번의 시도를 해야 최상의 수를 선택할 수 있다. 베어링 데이터의 경우 6가지의 라벨이 있다. (이는 군집수가 6개 정도는 되야 한다는 것이다) 선택받지 못한 3개의 라벨(unknown, failure.b1, failure.b2는 대체된 이름일 수 있으므로 포함하지 않는다.
하지만 b3와 b4는 그 양상이 서로 다르므로 라벨을 두 개 이상의 클러스터에 적용해야 한다. 9개의 라벨이 있기 때문에 18개까지 생각한다. 총 6-18까지 모든 k를 시도한다고 했을 때 모든 분석을 수동으로 한다면 꽤나 많은 시간이 걸릴 것이다. 모델의 적합성을 빠르게 계산하기 위해 다음과 같은 방식으로 구현한다.
k <- 8
means <- kmeans(data[,-c(1, 2)], k)kmeans 알아서 지정해주는 모양이다. 여기서 알아야 할 점은 feature = clustring 가 아니라는 것이다.
table(data.frame(data$State, means$cluster))
> table(data.frame(data$State, means$cluster))
means.cluster
data.State 1 2 3 4 5 6 7 8
early 0 343 305 167 0 332 156 44
failure.b1 57 0 0 0 0 0 0 0
failure.b2 29 2 0 0 1 3 0 2
failure.inner 0 0 0 0 37 0 0 0
failure.roller 233 14 0 0 158 0 0 0
normal 810 1290 0 985 0 515 0 889
stage2 0 20 0 0 297 0 0 0
suspect 725 214 0 0 116 120 0 310
unknown 146 0 6 0 0 0 0 298이렇게도 사용할 수 있다. 데이터를 살펴보면 early는 모든 곳에 고루게 분포하였지만 failure.b1은 1번 클러스터 에서만 나타나고 있다. 이는 정확성을 나타낸다는데 이 데이터로 결론을 내리기에는 어렵다. 라벨에 엮인 데이터의 수가 균일하지 않기 때문이다. 각 행을 백분율로 변환하고 전체를 함수로 매핑해본다.
calculate.confusion <- function(states, clusters)
{
# generate a confusion matrix of cols C versus states S
d <- data.frame(state = states, cluster = clusters)
td <- as.data.frame(table(d))
# convert from raw counts to percentage of each label
pc <- matrix(ncol=max(clusters),nrow=0) # k cols
for (i in 1:9) # 9 labels
{
total <- sum(td[td$state==td$state[i],3])
pc <- rbind(pc, td[td$state==td$state[i],3]/total)
}
rownames(pc) <- td[1:9,1]
return(pc)
}이후 클러스터에 라벨을 정해주기 위해서 두 가지 단계를 밟아야 한다. 첫번째로 모든 클러스터는 라벨을 가지고 있어야 한다. 할당 된 데이터 포인트의 비율이 가장 높은 라벨을 선택한다. 클러스터 3번과 7번이 'early' 라벨로 정해질 수 있다. 두번째로 모든 라벨은 적어도 하나의 클러스터와 연결되어 있어야 한다. 그렇지 않으면 k-means로는 라벨이 무엇인지 알 수가 없다. 클러스터에 할당되지 않은 모든 라벨을 클러스터에 할당한다.
assign.cluster.labels <- function(cm, k)
{
# take the cluster label from the highest percentage in that column
cluster.labels <- list()
for (i in 1:k)
{
cluster.labels <- rbind(cluster.labels, row.names(cm)[match(max(cm[,i]), cm[,i])])
}
# this may still miss some labels, so make sure all labels are included
for (l in rownames(cm))
{
if (!(l %in% cluster.labels))
{
cluster.number <- match(max(cm[l,]), cm[l,])
cluster.labels[[cluster.number]] <- c(cluster.labels[[cluster.number]], l)
}
}
return(cluster.labels)
}이 두 스텝을 이용하여 라벨의 결과 목록을 만들어낸다.
results <- matrix(ncol=2, nrow=0)
models <- list()
best.row <- match(max(results[,2]), results[,2])
best.kmeans <- models[[best.row]]
save(best.kmeans, file=paste0(basedir, "../kmeans.obj"))
k <- length(best.kmeans$size)
conf.mat <- calculate.confusion(data$State, best.kmeans$cluster)
cluster.labels <- assign.cluster.labels(conf.mat, k)
acc <- calculate.accuracy(data$State, cluster.labels[best.kmeans$cluster])
cat("For", k, "means with accuracy", acc, ", labels are assigned as:\n")
cat(str(cluster.labels))나타나는 리스트는 다음과 같다.
List of 8
$ : chr [1:4] "failure.b1" "failure.b2" "failure.roller" "suspect"
$ : chr "normal"
$ : chr "early"
$ : chr "normal"
$ : chr [1:2] "failure.inner" "stage2"
$ : chr "early"
$ : chr "early"
$ : chr "unknown"클러스터 1은 매자신의 라벨이 무엇인지 정확히 정하지 못했다. 클러스터 3,6,7은 early를 나타내고 있다. 클러스터와 라벨을 검사하여 얼마나 정확한지 비교한다.
calculate.accuracy <- function(states, clabels)
{
matching <- Map(function(state, labels) { state %in% labels }, states, clabels)
tf <- unlist(matching, use.names=FALSE)
return (sum(tf)/length(tf))
}정확도는 이제 6부터 18까지 범위 안의 k를 조사하여 어떤 것이 가장 정확한지 알아낸다.
results <- matrix(ncol=2, nrow=0)
models <- list()
for (k in 6:18)
{
# Don't cluster columns for bearing or State
means <- kmeans(data[,-c(1, 2)], k)
# generate a confusion matrix of cols C versus states S
conf.mat <- calculate.confusion(data$State, means$cluster)
cluster.labels <- assign.cluster.labels(conf.mat, k)
# Now calculate accuracy, using states and groups of labels for each cluster
accuracy <- calculate.accuracy(data$State, cluster.labels[means$cluster])
results <- rbind(results, c(k, accuracy))
models[[(length(models)+1)]] <- means
}Visualising the best model
가장 좋은 모델을 찾아 저장하자.
best.row <- match(max(results[,2]), results[,2])
best.kmeans <- models[[best.row]]
save(best.kmeans, file=paste0(basedir, "../../models/kmeans.obj"))이후 클러스터 수, 정확도 같은 핵심 정보를 출력해서 살펴본다.
k <- length(best.kmeans$size)
conf.mat <- calculate.confusion(data$State, best.kmeans$cluster)
cluster.labels <- assign.cluster.labels(conf.mat, k)
acc <- calculate.accuracy(data$State, cluster.labels[best.kmeans$cluster])
cat("For", k, "means with accuracy", acc, ", labels are assigned as:\n")
cat(str(cluster.labels))이제 라벨을 클러스터에 할당하면 데이터의 61%정도가 지정된 라벨이 있는 클러스터로 분류된다. 4개의 베어링을 순차적으로 그래프를 그려 데이터의 움직임을 살펴보자.
# use the same colours for states as before
cols <- do.call(rbind, Map(function(s)
{
if (s=="early") "green"
else if (s == "normal") "blue"
else if (s == "suspect") "darkgoldenrod"
else if (s == "stage2") "salmon"
else if (s == "unknown") "black"
else "red"
}, data$State))
# plot each bearing changing state
par(mfrow=c(2,2))
for (i in 1:4)
{
s <- (i-1)*2156 + 1 # 2156 datapoints per bearing
e <- i*2156
plot(best.kmeans$cluster[s:e], col=cols[s:e], ylim=c(1,k), main=paste0("Bearing ", i), ylab="Cluster")
}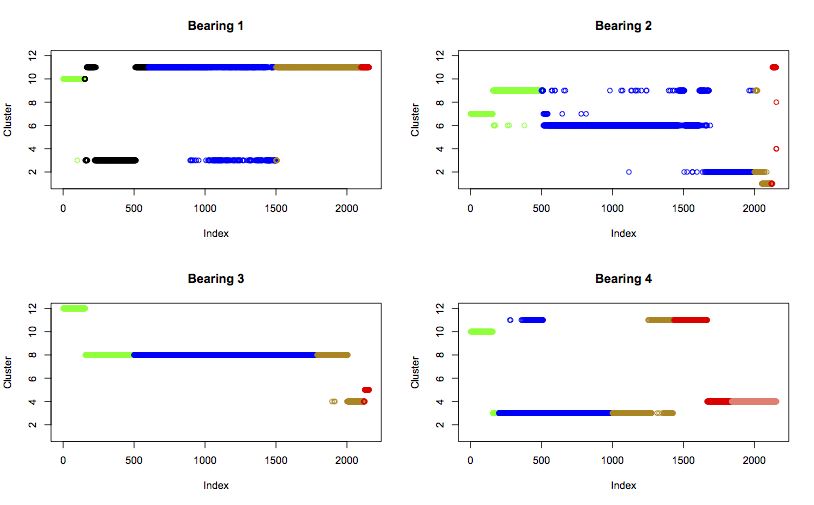
이제 클러스터 라벨과 비교하여 살펴본다.

Conclusion
데이터에 할당한 라벨은 클러스터에 비교적 적합해졌고 다음 번에는 분류자를 통해 패턴을 학습시켜 본다.
사용한 코드
b1 <- read.table(file=paste0(basedir, "../b1_all.csv"), sep=",", header=TRUE)
b2 <- read.table(file=paste0(basedir, "../b2_all.csv"), sep=",", header=TRUE)
b3 <- read.table(file=paste0(basedir, "../b3_all.csv"), sep=",", header=TRUE)
b4 <- read.table(file=paste0(basedir, "../b4_all.csv"), sep=",", header=TRUE)
# Bearing state classes (determined by eye)
b1.labels <- c(rep("early", times=150), rep("unknown", times=450), rep("normal", times=899), rep("suspect", times=600), rep("failure.b1", times=57))
b2.labels <- c(rep("early", times=499), rep("normal", times=1500), rep("suspect", times=120), rep("failure.b2", times=37))
b3.labels <- c(rep("early", times=499), rep("normal", times=1290), rep("suspect", times=330), rep("failure.inner", times=37))
b4.labels <- c(rep("early", times=199), rep("normal", times=800), rep("suspect", times=435), rep("failure.roller", times=405), rep("stage2", times=317))
b1 <- cbind(b1, State=b1.labels)
b2 <- cbind(b2, State=b2.labels)
b3 <- cbind(b3, State=b3.labels)
b4 <- cbind(b4, State=b4.labels)
best <- c("Min.x", "Median.x", "Max.x", "Mean.x", "Skew.x", "Kurt.x", "FTF.x", "BPFI.x", "BPFO.x", "BSF.x", "F2.x", "F3.x", "F4.x", "F5.x", "Min.y", "Max.y", "Skew.y", "Kurt.y", "FTF.y", "BPFI.y", "BPFO.y", "BSF.y", "F2.y", "F3.y", "F4.y", "F5.y", "Qu.1.x", "VHF.pow.x", "Qu.1.y", "Median.y", "HF.pow.y")
data <- rbind(
cbind(bearing="b1", (b1[,c("State", best)])),
cbind(bearing="b2", (b2[,c("State", best)])),
cbind(bearing="b3", (b3[,c("State", best)])),
cbind(bearing="b4", (b4[,c("State", best)]))
)
library("entropy")
# MI = H(x) + H(y) - H(x, y)
H.x <- entropy(table(data$State))
mi <- apply(data[, -c(1, 2)], 2, function(col) { H.x + entropy(table(col)) - entropy(table(data$State, col))})
# Now select the correct size of FV by testing different classifiers
library("rpart")
library("caret")
train.rows <- seq(1, length(data$State), by=4) # every fourth index
sorted <- names(sort(mi, decreasing=TRUE))
accuracies <- vector()
for (i in 2:length(sorted))
{
form <- paste0("data$State ~ data$", Reduce(function (r, name) { paste(r, paste0("data$", name), sep=" + ") }, sorted[1:i]))
model <- rpart(as.formula(form), data, subset=train.rows)
pred <- predict(model, data, type="class") # contains train and test set predictions
cm <- confusionMatrix(pred[-train.rows], data[-train.rows, 2]) # only the non-training rows
# pull out the answer
accuracies <- c(accuracies, cm["overall"][[1]]["Accuracy"][[1]])
}
plot(accuracies, xlab="Number of features", ylab="Accuracy")
# 14 features looks best. save those plus bearing and state labels
write.table(data[c("bearing", "State", sorted[1:14])], file=paste0(basedir, "../all_bearings_best_fv.csv"), sep=",", row.names=FALSE)
data <- read.table(file=paste0(basedir, "../all_bearings_best_fv.csv"), sep=",", header=TRUE)
k <- 8
means <- kmeans(data[,-c(1, 2)], k)
table(data.frame(data$State, means$cluster))
calculate.confusion <- function(states, clusters)
{
# generate a confusion matrix of cols C versus states S
d <- data.frame(state = states, cluster = clusters)
td <- as.data.frame(table(d))
# convert from raw counts to percentage of each label
pc <- matrix(ncol=max(clusters),nrow=0) # k cols
for (i in 1:9) # 9 labels
{
total <- sum(td[td$state==td$state[i],3])
pc <- rbind(pc, td[td$state==td$state[i],3]/total)
}
rownames(pc) <- td[1:9,1]
return(pc)
}
assign.cluster.labels <- function(cm, k)
{
# take the cluster label from the highest percentage in that column
cluster.labels <- list()
for (i in 1:k)
{
cluster.labels <- rbind(cluster.labels, row.names(cm)[match(max(cm[,i]), cm[,i])])
}
# this may still miss some labels, so make sure all labels are included
for (l in rownames(cm))
{
if (!(l %in% cluster.labels))
{
cluster.number <- match(max(cm[l,]), cm[l,])
cluster.labels[[cluster.number]] <- c(cluster.labels[[cluster.number]], l)
}
}
return(cluster.labels)
}
str(assign.cluster.labels(calculate.confusion(data$State, means$cluster), k))
for (k in 6:18)
{
# Don't cluster columns for bearing or State
means <- kmeans(data[,-c(1, 2)], k)
# generate a confusion matrix of cols C versus states S
conf.mat <- calculate.confusion(data$State, means$cluster)
cluster.labels <- assign.cluster.labels(conf.mat, k)
# Now calculate accuracy, using states and groups of labels for each cluster
accuracy <- calculate.accuracy(data$State, cluster.labels[means$cluster])
results <- rbind(results, c(k, accuracy))
models[[(length(models)+1)]] <- means
}
calculate.confusion <- function(states, clusters)
{
# generate a confusion matrix of cols C versus states S
d <- data.frame(state = states, cluster = clusters)
td <- as.data.frame(table(d))
# convert from raw counts to percentage of each label
pc <- matrix(ncol=max(clusters),nrow=0) # k cols
for (i in 1:9) # 9 labels
{
total <- sum(td[td$state==td$state[i],3])
pc <- rbind(pc, td[td$state==td$state[i],3]/total)
}
rownames(pc) <- td[1:9,1]
return(pc)
}
assign.cluster.labels <- function(cm, k)
{
# take the cluster label from the highest percentage in that column
cluster.labels <- list()
for (i in 1:k)
{
cluster.labels <- rbind(cluster.labels, row.names(cm)[match(max(cm[,i]), cm[,i])])
}
# this may still miss some labels, so make sure all labels are included
for (l in rownames(cm))
{
if (!(l %in% cluster.labels))
{
cluster.number <- match(max(cm[l,]), cm[l,])
cluster.labels[[cluster.number]] <- c(cluster.labels[[cluster.number]], l)
}
}
return(cluster.labels)
}
calculate.accuracy <- function(states, clabels)
{
# For each means$cluster c, if cluster.labels[[c]] contains data$State, it's correct
matching <- Map(function(state, labels) { state %in% labels }, states, clabels)
tf <- unlist(matching, use.names=FALSE)
return (sum(tf)/length(tf))
}
data <- read.table(file=paste0(basedir, "../all_bearings_best_fv.csv"), sep=",", header=TRUE)
results <- matrix(ncol=2, nrow=0)
models <- list()
best.row <- match(max(results[,2]), results[,2])
best.kmeans <- models[[best.row]]
save(best.kmeans, file=paste0(basedir, "../kmeans.obj"))
k <- length(best.kmeans$size)
conf.mat <- calculate.confusion(data$State, best.kmeans$cluster)
cluster.labels <- assign.cluster.labels(conf.mat, k)
acc <- calculate.accuracy(data$State, cluster.labels[best.kmeans$cluster])
cat("For", k, "means with accuracy", acc, ", labels are assigned as:\n")
cat(str(cluster.labels))
str(assign.cluster.labels(calculate.confusion(data$State, means$cluster), k))
cols <- do.call(rbind, Map(function(s)
{
if (s=="early") "green"
else if (s == "normal") "blue"
else if (s == "suspect") "darkgoldenrod"
else if (s == "stage2") "salmon"
else if (s == "unknown") "black"
else "red"
}, data$State))
par(mfrow=c(2,2))
for (i in 1:4)
{
s <- (i-1)*2156 + 1 # 2156 datapoints per bearing
e <- i*2156
plot(best.kmeans$cluster[s:e], col=cols[s:e], ylim=c(1,k), main=paste0("Bearing ", i), ylab="Cluster")
}
par(mfrow=c(2,3))
plot(Kurt.x ~ Skew.x, data=data, col=cols)
points(Kurt.x ~ Skew.x, data=best.kmeans$centers, pch=10)
plot(FTF.x ~ BPFI.x, data=data, col=cols)
points(FTF.x ~ BPFI.x, data=best.kmeans$centers, pch=10)
plot(BPFO.x ~ BSF.x, data=data, col=cols)
points(BPFO.x~ BSF.x, data=best.kmeans$centers, pch=10)
plot(FTF.y ~ BPFI.y, data=data, col=cols)
points(FTF.y ~ BPFI.y, data=best.kmeans$centers, pch=10)
plot(BPFO.y ~ BSF.y, data=data, col=cols)
points(BPFO.y ~ BSF.y, data=best.kmeans$centers, pch=10)
plot(VHF.pow.x ~ HF.pow.y, data=data, col=cols)
points(VHF.pow.x ~ HF.pow.y, data=best.kmeans$centers, pch=10)
'미분류 > R' 카테고리의 다른 글
| Understanding data science: more classification techniques (0) | 2019.06.13 |
|---|---|
| Understanding data science: classification with neural networks in R (0) | 2019.06.12 |
| R 기본 (추가 중) (0) | 2019.06.05 |
| Understanding data science: dimensionality reduction with R (0) | 2019.06.04 |
| Understanding data science:designing useful features with R (0) | 2019.06.03 |



